numpy.poly1d

class numpy.poly1d(c_or_r, r=False, variable=None) [source]

A one-dimensional polynomial class.

A convenience class, used to encapsulate “natural” operations on polynomials so that said operations may take on their customary form in code (see Examples).

Parameters:

c_or_r : array_like The polynomial’s coefficients, in decreasing powers, or if the value of the second parameter is True, the polynomial’s roots (values where the polynomial evaluates to 0). For example, poly1d([1, 2, 3]) returns an object that represents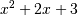 , whereas poly1d([1, 2, 3], True) returns one that represents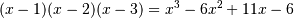 . r : bool, optional If True, c_or_r specifies the polynomial’s roots; the default is False. variable : str, optional Changes the variable used when printing p from x to variable (see Examples).

Examples

Construct the polynomial :

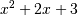>>> p = np.poly1d([1, 2, 3])
>>> print(np.poly1d(p))
   2
1 x + 2 x + 3

Evaluate the polynomial at :

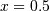>>> p(0.5)
4.25

Find the roots:

>>> p.r
array([-1.+1.41421356j, -1.-1.41421356j])
>>> p(p.r)
array([ -4.44089210e-16+0.j,  -4.44089210e-16+0.j])

These numbers in the previous line represent (0, 0) to machine precision

Show the coefficients:

>>> p.c
array([1, 2, 3])

Display the order (the leading zero-coefficients are removed):

>>> p.order
2

Show the coefficient of the k-th power in the polynomial (which is equivalent to p.c[-(i+1)]):

>>> p[1]
2

Polynomials can be added, subtracted, multiplied, and divided (returns quotient and remainder):

>>> p * p
poly1d([ 1,  4, 10, 12,  9])

>>> (p**3 + 4) / p
(poly1d([  1.,   4.,  10.,  12.,   9.]), poly1d([ 4.]))

asarray(p) gives the coefficient array, so polynomials can be used in all functions that accept arrays:

>>> p**2 # square of polynomial
poly1d([ 1,  4, 10, 12,  9])

>>> np.square(p) # square of individual coefficients
array([1, 4, 9])

The variable used in the string representation of p can be modified, using the variable parameter:

>>> p = np.poly1d([1,2,3], variable='z')
>>> print(p)
   2
1 z + 2 z + 3

Construct a polynomial from its roots:

>>> np.poly1d([1, 2], True)
poly1d([ 1, -3,  2])

This is the same polynomial as obtained by:

>>> np.poly1d([1, -1]) * np.poly1d([1, -2])
poly1d([ 1, -3,  2])

Attributes

c	A copy of the polynomial coefficients
coef	A copy of the polynomial coefficients
coefficients	A copy of the polynomial coefficients
coeffs	A copy of the polynomial coefficients
o	The order or degree of the polynomial
order	The order or degree of the polynomial
r	The roots of the polynomial, where self(x) == 0
roots	The roots of the polynomial, where self(x) == 0
variable	The name of the polynomial variable

Methods

__call__(val)
deriv([m])	Return a derivative of this polynomial.
integ([m, k])	Return an antiderivative (indefinite integral) of this polynomial.